一、田口的概念          

    傳統的品質觀念是符合規格(Meet the specification)，亦即二分法，在規格內的是好的，在規格外的是不好的，所以在規格內的沒有損失，在規格外的才會產生損失，用圖形表示為以下：



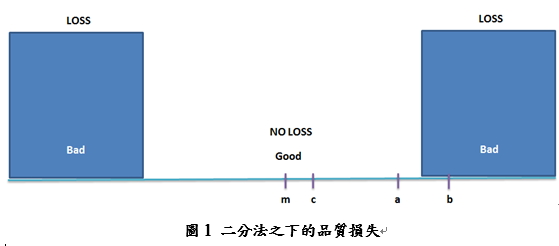
這樣的講法不好！為什麼？

1. 圖1中的a、b兩點所代表的品質特性真的有那麼大的差別嗎？

    例：以TFT-LCD的信賴性測試結果，假設有2台電視，一台的信賴性測試因為稍稍超出規格(如點b)而未能出廠，
另一台則因勉強合格(如點a)而出廠，但因很靠近規格上限，距離目標值m甚遠，所以很快就發生問題，以致顧客抱怨，而喪失市場！兩台品質相差無幾的電視機卻因判斷標準是符合規格與否而造成結果迥異，一出廠一未出廠，而產生的後果是更不利廠家。
    又例如：美國汽車在聯邦汽車安全標準(Federal Motor Vehicle Safety Standard；FMVSS)第207條款規定椅背必須能承受撞擊GM至少45次以上才能賣，所以如果用二分法，大於45次的可以出廠，否則不能出廠；則GM=45.1次的汽車真的能提供乘客的安全保護嗎？GM=45.1次與GM=49.5是否真的有顯著的差異嗎？

2. 不知是否仍有改善的餘地？

    在二分法之下，所有符合規格的都是良品，都沒有損失(如圖1)，而所有不合規格的，皆為不良品且損失相同，前面討論過a、b所代表的品質水準差別不大，但因是二分法的關係所以造成以為a比b好的作法(一個能出廠，一個不能出廠)固然不對；但說a與c是同樣的好(沒有損失)這也不對；因為目標值m，所以越接近m越好，所以c比a好；用損失函數可以很清楚地看出a、b、c的差別。

3. 公差累積(Tolerance Stack-up)的問題

    例如：精密工具機的傳動主軸，若是剛好通過規格下限，而外購來的軸承其孔徑非常靠近規格上限，則組合後的工具機能否達到原訂的精密度呢？因為兩者皆有偏離規格的中心值，所以一定不可能達到原來設計的精密度；當然這種情況在實務上還是否辦法補救
(聯想：有什麼辦法呢？)，但與其事後補救，不如事前儘量push你的製程達到目標值，我們在觀念上一定要有所突破！

4.規格的制訂合理嗎？

所以只是依照規格是不夠的，產品不但要合乎規格，而且要製造成本低，同時也要能不受外界環境的影響。這正是田口先生的貢獻；連接工程與統計方法來快速、有效地達到成本與品質的改進。
學習田口方法的好處可以說有下列幾點：

1) 能夠快速地達到成本與品質的改進。
2) 提供設計部門與製造部門一個“共同語言”。
3) 品管活動的目標若能跟“成本”密切連結，則品管可以成為公司管理的良好工具，而田口法正好具有此特點。

傳統的品質指標(Quality Measure)像是rework cost、scrap rate或Cp等都嫌太慢，品質應該是越早能評估越好(在產品的開發、設計階段)，因為這樣才較能發揮工程專業知識及突顯統計的功力；所以光憑工程師的經驗固然不妥，但統計學若只是在資料的轉換上大做文章亦屬可惜！工程師需要統計知識恰如統計學者需要工程品味一樣；工程師需要一些具有工程意義(Engineering sense)或工程認可(Engineering justifiable)的統計方法，我認為這是貫穿田口先生所提出的各種方法的一個出發點；另外一個貫穿田口的則是事前的主動出擊，而不是事後的被動回應。


二、田口先生對品質的定義    


田口先生的品質定義就是所有的不良品皆為社會損失，到底什麼是社會損失？值得我們再多作一些說明。我們將藉著3個例子來解釋社會損失，並且瞭解在制訂公差上的應用。

例一：聚乙烯膜厚度的問題

    聚乙烯膜是用來覆蓋溫室的，主要作用是要保護溫室內的農作物不受惡劣氣候(雪、風以及雨等)的影響，所以膜的厚度一定要夠；但是太厚又會阻擋陽光的照射，所以又不能太厚；當時日本政府規定的厚度規格為1mm+0.2mm，但對製造聚乙烯膜的廠商而言當然是越薄越好，因為單位製造成本會降低；所以當廠商知道他自己的製程能力已經達到能控制製程變異到+0.02mm時，就做了一個合乎本身利益的決定—把厚度的Nominal值由1mm降到0.82mm，則他所生產膜的厚度範圍是0.82mm+0.02mm (0.8mm~0.84mm)，仍然是符合政府規格的；但是這樣做的結果是，當年日本刮颱風，溫室缺乏適當的保護，所造成的損失有：

1. 聚乙烯膜製造商的損失，因為膜被吹壞要賠償農民。
2. 農民的損失，因為農作物被損壞殆盡。
3. 社會損失，因為農作物歉收，引起物價上揚，造成整個市場價格波動。

例二：電話電纜銅線粗細問題

    用在電話電纜的銅線它的電阻值應該是m+∆ (歐姆/哩)；但假設拉銅線的製程能力大幅提升，製程變異甚至小於∆，所以廠商把銅線的電阻值的Nominal值增大但仍維持在+∆之內，則銅線變細，製造成本下降，但從網路的角度來看，高電阻造成的電力損失以及客戶抱怨，後續的修補成本遠大於製造成本的節省。
    以上兩個例子說明一件事，只要求符合規格(Meeting the tolerance)是不夠的，一定要命中目標(Meeting the target)才行！！

    接下來，我們看另一個例子說明損失函數在製程公差設計上的應用。

例三：電視機線路問題

    電視機裡面有一條線路是將100伏的交流電轉換成115伏的直流電，所以目標值m=115伏；但若輸出電壓偏離115伏，降至90伏以下時，則會影像模糊，對比太弱無法調整，整條線路需要修理或更換整台電視機；昇至140伏以上時又會使對比太強，同樣的需要修理或更換。假設消費者對兩種偏離的容忍度是一樣的，再假設當電壓真的低於90伏或高於140伏，50%的消費者會失去耐心而要求修理或更換(費用是30,000元)，則消費者的損失函數L(y)=k(y-115)²，其中的k可以由30000=k ╳ 25²算出，k=30000/25²=48，所以消費者損失函數為L(y)=48(y-115)²。

    一般來講，生產部門或是製造單位的工程藍圖上的公差跟消費者的公差是不一樣的，因為因製程變異所造成的不合格品通常可以在工廠裡再製造或甚至丟棄而所造成的總損失較小。在本例中，線路的輸出電壓可以經由電阻器變換而改善，譬如，通常是用50KΩ的電阻器的話，則每降1KΩ，電壓值可以增高0.5伏，所以用50KΩ的電阻通上100伏的交流電，若輸出電壓是112伏，則改用44 KΩ的電阻器就可以將輸出電壓調升至目標值115伏，若電阻的成本是10元，而換裝的工作大約須2~3小時工時，則整個調整成本約為100元；假使製造單位不願意花100元來調整，理由是112伏仍在消費者的公差範圍，則這台電視機會對消費者造成L(y)=48(112-115)²=432(元)的損失，為了節省100元而讓消費者承擔432元的損失，這種行為田口先生認為是比強盜更壞的行為；因為從社會損失的角度來看，製程公差是當二者平衡時所決定的，所以：100=48(y-115)²→y=115+1.4製程公差應是+1.4伏，而不是消費者所能容忍的+25伏，112不在115+1.4之內，所以根本不應該出廠，認為其符合消費者公差自屬不當。